미분 겉핥기
미분은 미분 微分 이라고 쓴다. 작게 나눈다 라는 뜻인데. 함수의 변화량을 아주 작은 구간으로 나눈다는 말이다.
전에 글에서 이야기 했던 평균변화율을 구하는 구간을 점점 줄여가서 결국 한 점으로 줄여 순간의 변화율을 구하는 것을 미분한다고 한다.
이 변화율이라는것은 좌표 평면상의 두 점에서 x값이 증가한것 분에 y값이 증가한 분량이다.
결국 변화율은 두 점사이를 잇는 직선의 기울기 이다. 그러므로 순간변화율을 구한다 라는것은 그 한점의 접선의 기울기를 구한다 라는것이고 그 말이 바로 미분한다 라는 말의 의미이다.
미분한다 라는 의미
미분한다 라는것은 한점의 접선의 기울기를 구하는것이다.
한 곡선을 생각해보자, 예를들어 좌표평면 상에 영어 U자형의 그래프가 있다고 했을 때, 그 위에 있는 한점을 상상하고 그 점을 지나면서 2차함수와는 그 딱 한점과만 만나는 직선을 상상해보자. ( U/ ) 이렇게 생겼다고 가정하자. 바로 이 직선의 기울기를 구하는 것이 미분을 한다고 하는것이다.
그렇다면 어떠한 함수 f(x)를 좌표평면에 표시하고(그리고) f(1),f(2),f(3)…f(16),f(17) 등 임의의 값의 기울기를 구하기 위해서는 매번 평균변화율에 x값을 대입해서 극한을 사용해서 구해야 하는걸까.
도함수를 이용하자
순간변화율을 미분계수라는 용어로 부르고 미분계수는 f’(x)로 나타낸다.
연속적인 x값을 대입하여 미분계수(순간변화율)를 구하는 대신에 미지수를 대입하여 나온 미분계수의 값으로 새로운 함수를 만들 수 있다. 그리고 그 함수에 임의의 x값을 넣어도 바로바로 기울기를 구할 수 있을 것이다. 그렇게 임의의 x값에대한 순간변화율을 도함수 라고 한다.
예를 들어f(x) = x² 이라는 함수가 있다면
순간 변화율을 구하는 방법은
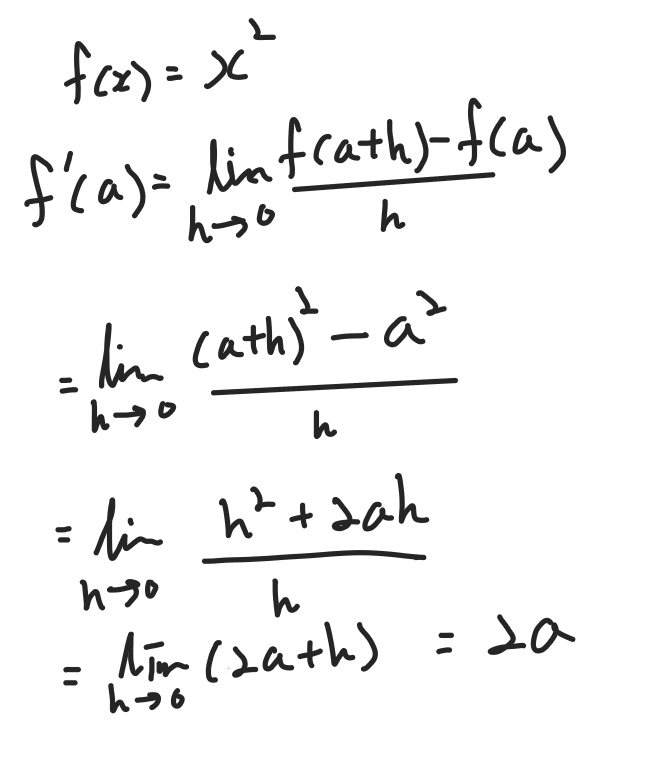
따라서 f(x) = x²의 도함수는 f'(x) = 2x이다.
이를 확장하면 도함수를 구하는 공식은 원래 함수의 차수를 계수와 곱해주고 원래 차수는 -1 하는것이다.
예를 들어 f(x)=4x³ 의 도함수를 구한다면
차수 3을 계수 4와 곱해주고(12), 원래 차수는 -1 해서 12x²이 된다.
도함수의 도는 유도하다 라는 뜻이고, 영어로는 파생된 이라는 뜻을 가진 derivative 이다. 파생된 함수라는 뜻이다. 우리는 도함수를 이용하여 그래프 상의 어떤 점에서라도 기울기를 구할 수 있다.
테마1 바로가기
https://strix1.mycafe24.com/줄글수학미분_테마1_변화율/